Doing regular multiplication quickly and without any tools may seem complex. However, one can become proficient in it with the help of proper guidance. This article will help you and your students understand Japanese multiplication, which helps overcome difficulties in solving mathematical problems and makes them fun. Once you master this method, you’ll do multiplication within seconds!
Grab a paper and a pencil so you can draw and practice while reading this guide! Visualization of the process is crucial for learning and moving forward.
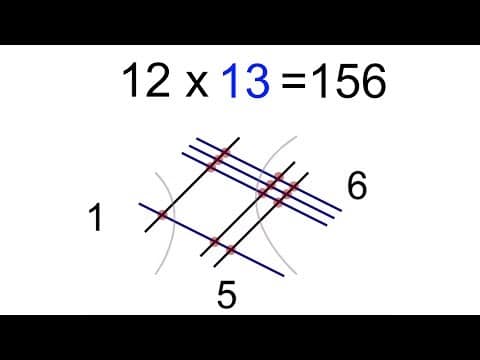
6 X 3
- Multiplication Lines – Draw a set of parallel lines that represent the numbers in the question. Suppose you have to solve 6 x 3; this means you have 6 groups of 3, which is the same as 6 times 3. The number in front corresponds to the number of rows you have to draw, and the next number will be the number of columns.
- Once you have drawn the parallel lines corresponding to the numbers, you’ll have 6 vertical lines and 3 horizontal lines passing through it.
- Next, count the number of intersections happening with these lines. Mark these intersections as dots. Here, an intersection means the point where two lines meet or connect.
- Count the total number of intersections. Well, the number of dots I calculated on my sheet of paper is 18.
Did you get this answer? If yes, then it means you have done Japanese multiplication correctly. Good job!
If not, then don’t worry! You just need more practice. Let’s try a different question.
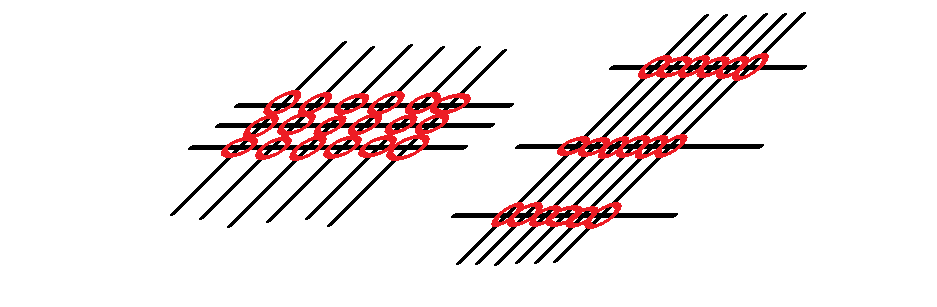
You need to keep in mind that the lines will get more complicated as you deal with bigger numbers. However, practice makes perfect!
Let’s try multiplying two-digit numbers!
Consider this problem:
23 x 21
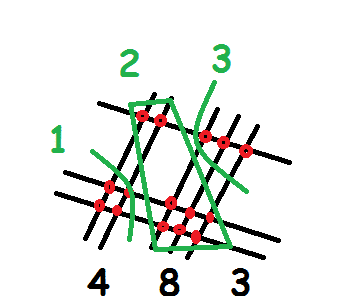
- Draw parallel lines that correspond to each number. First, start with 23, make 2 vertical lines, give some space, and draw 3 vertical lines beside them.
- Now draw horizontal lines that correspond with the second number in the question, i.e., 21. Hence, make 1 horizontal line crossing the vertical lines for 2 and 3 you drew in the previous step. Leave some space, and make 2 horizontal lines crossing the previous horizontal lines.
- Now, mark the intersections as dots. Write the number of times they are crossing at each corner.
- Count the dots in the bottom-left corner, and this will add up to 4 for this example.
- Then, count the dots in the top-left and bottom-right and add them. For this example, you’ll have 2 and 6, which add up to 8.
- Lastly, add the dots in the top-right corner, which adds up to 3.
- Now, read these numbers in the order you found them. You’ll get the answer for 23 x 21, which is 483.
Even if you have large numbers, don’t fret because the core principle of solving this is the same.
Make the parallel lines corresponding to the numbers, and mark intersections as dots. Count the dots in the bottom-left corner, add the dots in the top-left and bottom-right corners, and count the top-right corner. Arrange the digits in this order, and you will get your answer.
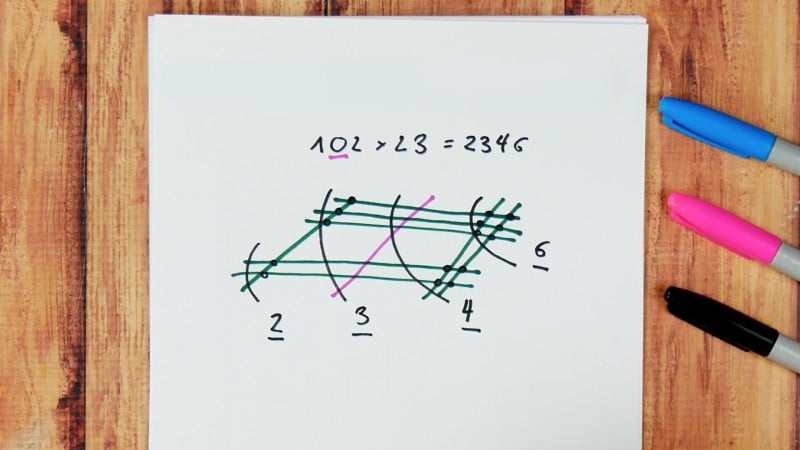
What to do when you have a zero in the question?
Suppose you need to multiply 102 with 23. Don’t draw a line for the zero this time because none of the intersections with zero will be counted. But if you want to simplify the question for yourself, then go ahead and draw a line in a different color but don’t count any dots that are passing through this line. Make dots at intersections and count them at each corner; however, don’t add the top-left and bottom-right dots. Instead, write them as digits with top-left dots first, followed by bottom-right dots.
Math solutions are not that difficult once you get the hang of them. They all follow a simple rule, and the steps are more or less the same for all. However, it’s always better to familiarize yourself with other quicker methods that would lead you to the answer as quickly as possible.
Most tests and classwork is standardized and timed. You might learn this method in school, and it’ll be a great tool in your arsenal. If not, then learning a novel method will do you no harm. It will only make you more knowledgeable. Hopefully, this article will help you master this technique.
On the other hand, it is possible to try this method, watch YouTube videos on it, read articles like this, and still not understand. Don’t stress out or lose motivation; there are many other ways to do quick multiplication. Check out some fun math tricks here!
There is no hard and fast rule for understanding mathematics. I struggled with this subject quite often. However, the key to becoming better is to do whatever makes you comfortable. Try different techniques, and ask your teacher for assistance and ways to make understanding math simpler for you and your classmates. Keep trying, and don’t give up!
Practice Examples
To reinforce your understanding of Japanese multiplication, it’s beneficial to practice with various examples. Here are a few more practice problems to help you master the technique:
- Example 1: 17 x 14
- Example 2: 35 x 29
- Example 3: 68 x 52
Take your time to draw the parallel lines, mark the intersections, and count the dots in each corner. Practicing these examples will further solidify your grasp of Japanese multiplication.
Advantages and Limitations
Japanese multiplication offers several advantages. It simplifies complex multiplication problems, enhances mental calculation skills, and enables quicker calculations. By visualizing the lines and intersections, you can break down the multiplication process and arrive at the solution efficiently. It’s an excellent technique to have in your mathematical toolbox.
However, it’s important to note that while Japanese multiplication is effective for certain scenarios, it may not always be the most suitable method. For larger calculations or situations that require a more structured approach, the traditional multiplication algorithm taught in schools might be more appropriate. It’s beneficial to be familiar with both methods and choose the one that best suits the specific calculation and context.
Real-World Applications
Japanese multiplication can be applied in various real-life situations. Consider the following examples:
-
Estimating Costs: When shopping, Japanese multiplication can help you quickly calculate the approximate total cost of multiple items at different prices. By multiplying the quantity of each item by its respective price, you can get a rough estimate of your expenses.
-
Quantity Calculation: In scenarios where you need to determine the total number of items arranged in multiple rows and columns, Japanese multiplication provides a speedy solution. By drawing the parallel lines and marking the intersections, you can swiftly count the dots in each corner to obtain the total quantity.
These are just a few instances where Japanese multiplication can be useful beyond academic settings. Its practical applications extend to various fields and day-to-day calculations.
Comparison with Traditional Method
In comparison to the traditional multiplication algorithm, Japanese multiplication offers some distinct advantages. While the traditional method involves carrying and aligning digits, Japanese multiplication simplifies the process by breaking down the numbers into intersecting lines. This approach allows for quicker mental calculations, especially with smaller numbers.
However, it’s essential to understand that the traditional algorithm remains a valuable tool, particularly for larger calculations and when a more structured approach is required. Both methods have their merits, and being proficient in both allows you to choose the most appropriate one based on the specific calculation and context.
Resources for Further Learning
If you’re interested in exploring Japanese multiplication further or learning additional mental calculation techniques, here are some recommended resources:
-
Book: “Secrets of Mental Math” by Arthur Benjamin and Michael Shermer. This book provides valuable insights into various mental math techniques, including Japanese multiplication.
-
Website: www.mathisfun.com – This website offers interactive math tutorials and exercises for various topics, including mental math techniques. It’s a great resource to deepen your understanding and improve your mathematical skills.
By leveraging these resources, you can expand your knowledge of mental calculation techniques and continue to enhance your mathematical abilities.
Remember, practice and exploration are key to becoming comfortable with mathematics. Keep trying different techniques, seek guidance from your teacher, and never hesitate to explore alternative methods that work best for you. With determination and perseverance, you’ll continue to improve and succeed in your mathematical journey.


